在益智玩具汉诺塔中,为了移动圆盘,玩家总是需要先移动一个塔上最上层的圆盘。而移动到下一个塔后,那个圆盘则始终会出现在那个塔的最上方。
这种后进先出 (Last-In, First-Out, LIFO ) 的操作模式,就是栈 (Stack) 的核心特征。
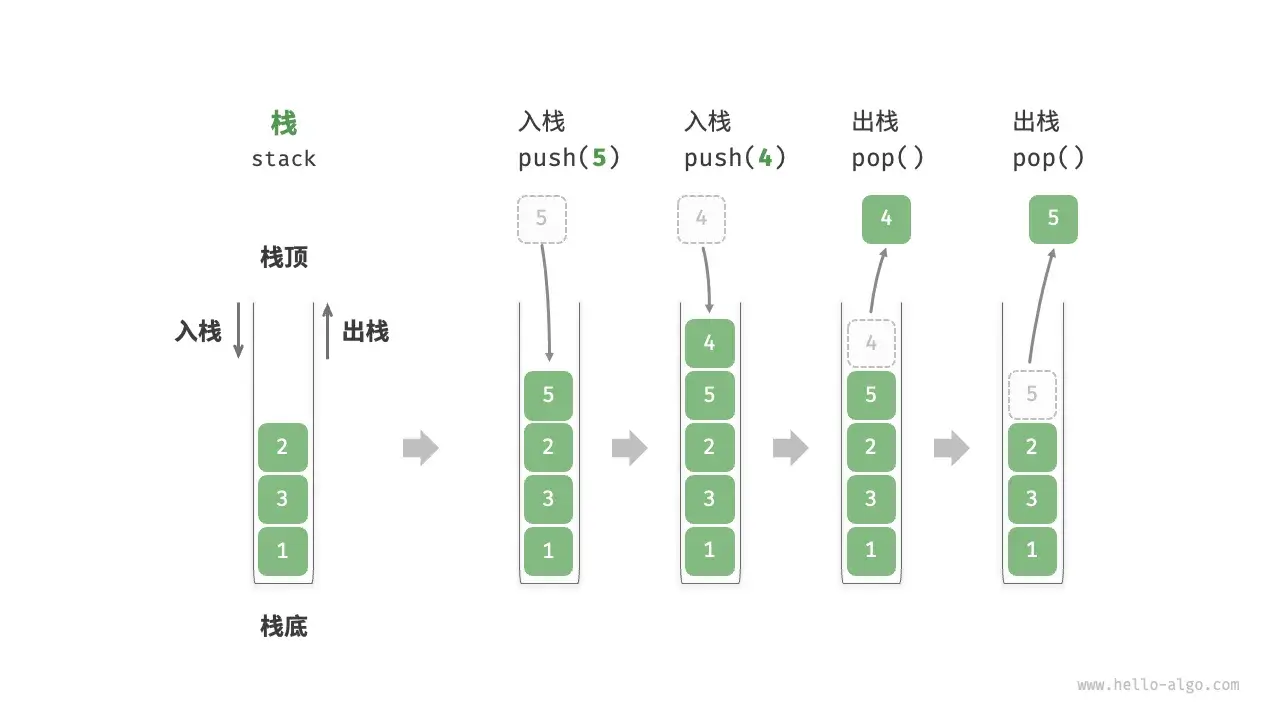
栈可以被视为一种受限的线性表,它只允许在表的一端(栈顶 )进行插入和删除操作:
入栈 (Push) :将元素添加到栈顶。出栈 (Pop) :移除并返回栈顶元素。栈顶 (Top) :允许操作的一端。栈底 (Bottom) :不允许操作的固定端。 在 .NET BCL 中,System.Collections.Generic.Stack<T> 是基于数组 实现的标准栈结构。其核心操作时间复杂度均为 O(1)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Stack<int > stack = new Stack<int >(); stack.Push(1 ); stack.Push(4 ); stack.Push(5 ); int peek = stack.Peek(); int pop = stack.Pop(); if (stack.TryPop(out int result)){ Console.WriteLine(result); } int count = stack.Count;
栈可以通过数组 (顺序栈)或链表 (链式栈)来实现。
我们可以利用 List<T> (动态数组) 来模拟栈。关键在于将数组的尾部作为栈顶 。
为什么不把数组头部当做栈顶?O(n);而在尾部操作只需要 O(1)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class ArrayStack <T >{ private List<T> _stack = []; public void Push (T item ) public int Count => _stack.Count; public bool IsEmpty => _stack.Count == 0 ; public T Peek () { if (IsEmpty) throw new InvalidOperationException("Stack is empty" ); return _stack[^1 ]; } public T Pop () { var item = Peek(); _stack.RemoveAt(_stack.Count - 1 ); return item; } }
使用单链表实现时,我们将链表头节点 (Head) 视为栈顶 。O(1) 操作,且无需像数组那样扩容。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 public class Node <T >(T value ){ public T Value { get ; set ; } = value ; public Node<T>? Next { get ; set ; } } public class LinkedStack <T >{ private Node<T>? _top = null ; private int _count = 0 ; public void Push (T item ) { var newNode = new Node<T>(item); newNode.Next = _top; _top = newNode; _count++; } public T Pop () { if (_top == null ) throw new InvalidOperationException("Stack is empty" ); T value = _top.Value; _top = _top.Next; _count--; return value ; } public T Peek () { if (_top == null ) throw new InvalidOperationException("Stack is empty" ); return _top.Value; } public bool IsEmpty => _count == 0 ; public int Count => _count; }
特性 基于数组 (List<T>) 基于链表 (LinkedList) 内存占用 较低 (紧凑存储) 较高 (每个节点需存储 Next 引用) 缓存友好性 高 (连续内存,CPU 缓存命中率高)低 (分散内存) 扩容开销 偶有 (需要扩容和复制) 无 (动态申请节点) 性能表现 通常更好 (.NET 默认 Stack<T> 采用此方案)稳定 (无扩容抖动)
函数调用栈 (Call Stack) :递归 (Recursion) 的基础。
表达式求值与语法解析 :(( )))、将中缀表达式转换为后缀表达式(逆波兰表示法)以及计算表达式的值。
浏览器的历史记录 :
撤销 (Undo) 操作 :Ctrl+Z 时,最近的一次操作出栈并被反向执行。
本文和右下角标有www.hello-algo.com标识的图片采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议,转载请注明出处。