UBC - CPSC 110 - Binary Search Trees

在一个列表中寻找元素是一个很简单的需求，但在实际生活中，它的数据量往往非常庞大。这时候我们就需要考虑性能这一要求，使用更高效的数据结构来提高查找效率。

这个新的自我引用数据结果就是二叉搜索树。 (Binary Search Tree, BST)

我们将围绕 BST 设计数据定义和函数，所用的知识和往常无异，当然，递归也是会被经常用到的。

学习目标

能够非正式地推理搜索数据所需的时间
能够识别适合用二叉搜索树表示的问题域 (problem domain) 信息
能够检查给定树是否符合二叉搜索树的不变式
能够运用设计方法进行二叉搜索树的设计

以下内容涉及到的edX链接均不保证可访问性

List Abbreviations

在研究 BST 之前，介绍一个定义列表的简便方法，比连着写一串cons更好看。比如说，对于(cons "a" (cons "b" (cons "c" empty)))，我们可以把它写成(list "a" "b" "c")。

Choose Language

记得在 DrRacket 的左下方，将Beginning Student切换为Beginning Student with List Abbreviations。

选择语言

切换后，运行刚刚的cons和list你会得到相同的结果：

1 2	(list "a" "b" "c") (list "a" "b" "c")

那我们之前为什么要费劲写这么多cons？只是为了介绍递归的概念不得不做的事。在熟悉它们后，自然就可以切换到更简单的写法了。

list表达式可以传入多个元素，而不仅仅是两个。同时，构建时里面的表达式也会被计算，比如：

1 2	(list (+ 1 2) (+ 3 4) (+ 5 6)) > (list 3 7 11)

行为不同

和cons不同，它的拼接过程本质不一样。cons在将元素和列表合并的时候，会将元素插入列表的首位。而list会将列表视为一个整体，将列表放到元素之后：

(cons "a" (list "b" "c"))
> (list "a" "b" "c")

(list "a" (list "b" "c"))
> (list "a" (list "b" "c"))

如果想让list达到相同效果，可以使用append表达式：

1 2	(append (list "b" "c") (list "d" "e" "f")) > (list "b" "c" "d" "e" "f")

List of Account & Binary Search Trees

在面对大量用户信息时，使用列表来存储和管理这些信息是一个常见的做法。我们可以使用二叉搜索树来优化对这些用户信息的查找和管理。下载来自edX的 lookup-in-list-starter.rkt 文件开始。

观察代码文件的内容，account含有字段num和name，所以对于一个用户列表来说，它可以是(list (make-account 1 "abc") (make-account 4 "dcj") (make-account 3 "ilk") (make-account 7 "ruf"))

虽然这里只有4个用户，但当用户数量非常非常多（几十上百万个）时，我们该如何根据用户的num来查找它的名字呢？以往的遍历耗时将会很长。（特别是当要查找的用户好巧不巧在末尾）

当然，运气好的话在一开始找到也是可能的，所以平均下来我们需要查找n/2个用户，这对于很大的用户量是完全不满足的。

考虑一个用户列表（为了简化表达，诸如(make-account 10 "why")会被简化为10:why）：(list 1:abc 3:ilk 4:dcj 7:ruf 10:why 14:olp 27:wit 42:ily 50:dug)。

首先，它是个有序列表（无序也得将其变成有序的），然后从中间元素（10:why）拆开，左边是(list 1:abc 3:ilk 4:dcj 7:ruf)，右边是(list 14:olp 27:wit 42:ily 50:dug)。保证在中间元素左边列表的num都比它小，右边列表的num都比它大。

以此类推，对之后的每个左侧和右侧列表执行这样的操作，就能得到一个树状图：

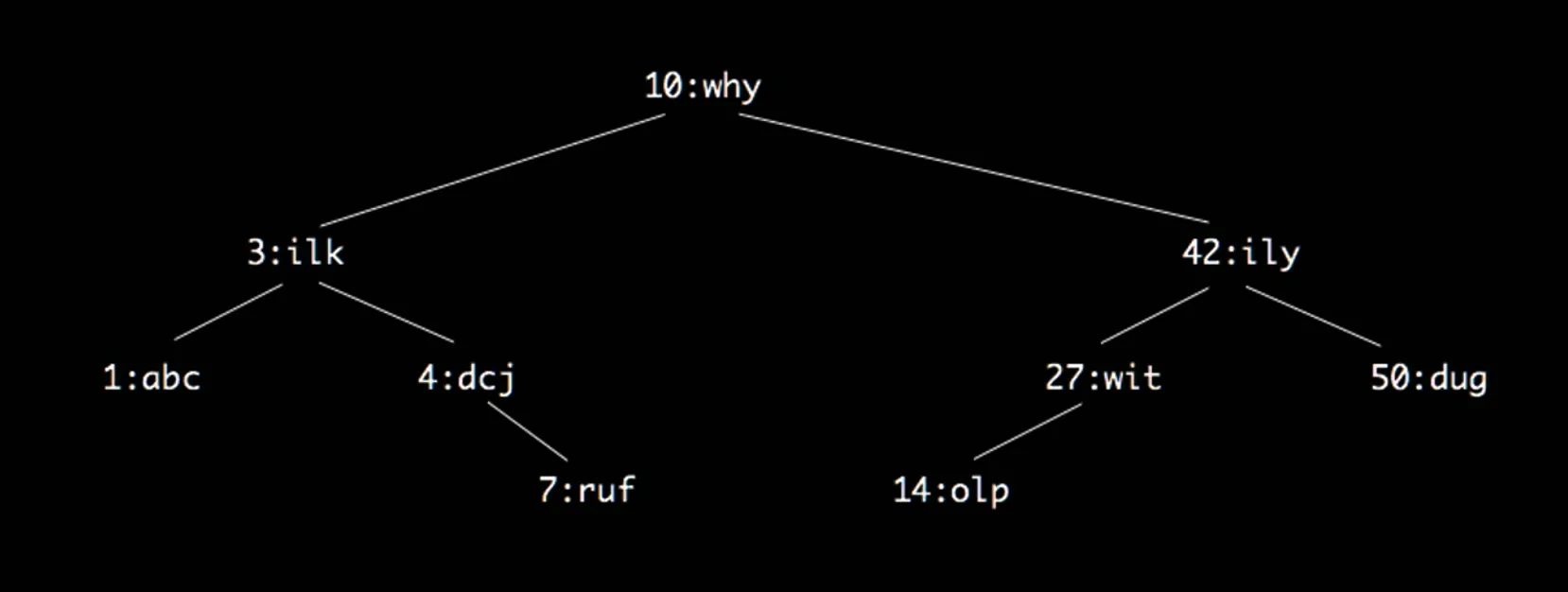
二叉搜索树

这里引用下我在.NET 数据结构：二叉树的概念与基本操作中的图：

二叉树结构示意图

BST

二叉搜索树属于二叉树 (Binary Tree)，它是一种特殊的二叉树，具有以下性质：

每个节点都有一个值（key），并且每个节点的值都大于其左子树中所有节点的值。
每个节点的值都小于其右子树中所有节点的值。
左右子树也都是二叉搜索树。

这种结构使得在平均情况下，极大地提高了查找、插入和删除操作的效率。

回到这个 BST 本身，假如我们要寻找num为14的用户，我们可以从根节点10:why开始：

发现14比10大，所以应该往右子树走，进入到42:ily
发现14比42小，所以应该往42:ily的左子树走，进入到27:wit
发现14比27小，所以应该往27:wit的左子树走，进入到14:olp
发现14:olp刚好是我们需要的数据

这样，我们就将平均搜索次数从n/2降低到了log n。

A Data Definition for BSTs

了解 BST 的机制和原理之后，这一节要求我们实现一个 BST 数据结构。下载来自 edX 的 bst-dd-starter.rkt 文件。

bst-dd-starter.rkt

观察注释块，它提供了一个 BST 的例子。实际上这个数据结构是由节点组成的，每个节点包含一个键值对和指向左右子树的引用，所以其本质上就是个复合数据类型：

键 (Key)：用于查询，在这里是num。
值 (Value)：与键对应的用户信息，在这里是name。
左子树 (Left Subtree)：指向当前节点左侧的子树，包含所有小于当前节点键的值。
右子树 (Right Subtree)：指向当前节点右侧的子树，包含所有大于当前节点键的值。

姑且将这个复合数据类型称为node，它包含key、val、l和r。但并不是每个节点都有左右子树，因此我们需要对l和r做一些特殊处理。

1	(define-struct node (key val l r))

同时需要定义组成这些node的树，我们可以将其定义为BST，它可以是一个node，也可以是false（空树）。这样就能处理子树可能为空的问题。同时存在一个约定，左右子树的值都要比父节点小或大。

;; BST (Binary Search Tree) is one of:
;;   - false
;;   - (make-node Integer String BST BST)
;; interp. false means no BST, or empty BST
;;         key is the node key
;;         val is the node value
;;         l and r are left and right subtrees
;; INVARIANT: for a given node:
;;     key is > all keys in its l(eft) child
;;     key is < all keys in its r(ight) child
;;     the same key never appears twice in the tree

它的例子如下：

(define BST0 false)
(define BST1 (make-node 1 "abc" false false))
(define BST4 (make-node 4 "dcj" false (make-node 7 "ruf" false false)))
(define BST3 (make-node 3 "ilk" BST1 BST4))
(define BST42 
  (make-node 42 "ily"
             (make-node 27 "wit" (make-node 14 "olp" false false) false)
             (make-node 50 "dug" false false)))
(define BST10
  (make-node 10 "why" BST3 BST42))

考虑到 BST 的函数模板可能需要处理空树或是在有节点的情况下四个字段的信息。需要注意的是，node的左右子树需要被传入回函数进行递归：

#;
(define (fn-for-bst t)
  (cond [(false? t) (...)]
        [else
         (... (node-key t)    ;Integer
              (node-val t)    ;String
              (fn-for-bst (node-l t))
              (fn-for-bst (node-r t)))]))

;; Template rules used:
;;  - one of: 2 cases
;;  - atomic-distinct: false
;;  - compound: (make-node Integer String BST BST)
;;  - self reference: (node-l t) has type BST
;;  - self reference: (node-r t) has type BST

至此，BST 的数据定义完成了。

Lookup in BSTs

如果你的进度中断了，可以下载来自edX的 lookup-in-bst-starter.rkt 文件开始。

lookup-in-bst-starter.rkt

本节会实现一个用于在 BST 中查询信息的函数，通过键找到对应的值。当然，并不是所有的键都有对应的值，因此我们需要处理查找失败的情况。

函数的签名是：;; BST Natural -> String or false，目的是;; Try to find node with given key, if found produce value; if not found produce false.

其测试需要照顾到返回值或者false的情况：

(check-expect (lookup-key BST0  99) false)
(check-expect (lookup-key BST1   1) "abc")
(check-expect (lookup-key BST1   0) false)
(check-expect (lookup-key BST1  99) false)
(check-expect (lookup-key BST10  1) "abc")  ;L L
(check-expect (lookup-key BST10  4) "dcj")  ;L R
(check-expect (lookup-key BST10 27) "wit")  ;R L
(check-expect (lookup-key BST10 50) "dug")  ;R R

将函数模板拷过来，改名。模板本身接受的是树，但我们同时需要查询值，所以需要加一个k表示键：

(define (lookup-key t k)
  (cond [(false? t) (...)]
        [else
         (... k
              (node-key t)    ;Integer
              (node-val t)    ;String
              (fn-for-bst (node-l t) (... k))
              (fn-for-bst (node-r t) (... k)))]))

对于空树的情况，或者说是查询到底了也没找着，自然就返回false。否则就进入到一个cond判断，如果当前节点的key等于查询的k，就返回当前节点的val。如果小于，就递归到左子树继续查找；如果大于，就递归到右子树继续查找：

(define (lookup-key t k)
  (cond [(false? t) false]
        [else
         (cond [(= k (node-key t)) (node-val t)]
               [(< k (node-key t)) (lookup-key (node-l t) k)]
               [(> k (node-key t)) (lookup-key (node-r t) k)]
               [else (...)])]))

else的存在是为了程序的健壮性，尽管在正常情况下不应该到达这个分支。

至此8个测试都通过了，我们成功实现了这个函数。

Rendering BSTs

本节将会尝试把二叉搜索树渲染出来，在此之前，下载来自 edX 的 render-bst-starter.rkt 文件。

render-bst-starter.rkt

这个文件已经把节点和树定义好了，留给我们一个问题：设计一个函数，接受一棵 BST，返回它的简易渲染图像。

BST 的图像应该很熟悉了，就是多个节点之间用线连接。那我们该怎么做呢？

我们可以效仿 BST 的搜索过程，也从每个节点出发寻找它的左右子树，将左右子树的渲染留给下一次递归。左右子树之间是有间隔的，它们也和父节点之间有一定的距离：

示意图

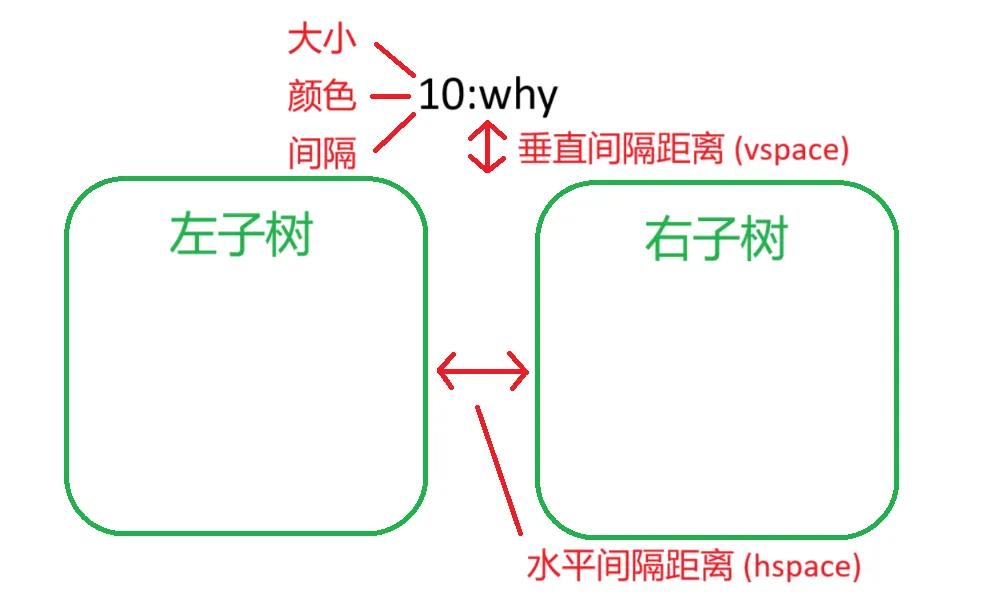
至此，我们需要定义一些常量：

字体大小和颜色
键值对之间的分隔符 (图里是:)
节点与左右子树之间的垂直间隔距离
左右子树之间的水平间隔距离
空树的占位图 (很容易被忽视)

;; Constants:

(define TEXT-SIZE 14)
(define TEXT-COLOR "black")

(define KEY-VAL-SEPARATOR ":")

(define VSPACE (rectangle 1  10 "solid" "white"))
(define HSPACE (rectangle 10  1 "solid" "white"))

(define MTTREE (rectangle 20 10 "solid" "white"))

接下来是函数设计，接受BST得到Image，获得一个简单的树图：

1 2	;; BST -> Image ;; produce a SIMPLE rendering of the tree

写测试的时候就得把图像结构构思出来了：节点和子树用above，子树之间用beside，中间隔一下就行。

(check-expect (render-bst false) MTTREE)
(check-expect (render-bst BST1) (above (text (string-append "1" KEY-VAL-SEPARATOR "abc")
                                             TEXT-SIZE
                                             TEXT-COLOR)
                                       VSPACE
                                       (beside (render-bst false)
                                               HSPACE
                                               (render-bst false))))
(check-expect (render-bst BST4) (above (text (string-append "4" KEY-VAL-SEPARATOR "dcj")
                                             TEXT-SIZE
                                             TEXT-COLOR)
                                       VSPACE
                                       (beside (render-bst false)
                                               HSPACE
                                               (render-bst (make-node 7 "ruf" false false)))))
(check-expect (render-bst BST3) (above (text (string-append "3" KEY-VAL-SEPARATOR "ilk")
                                             TEXT-SIZE
                                             TEXT-COLOR)
                                       VSPACE
                                       (beside (render-bst BST1)
                                               HSPACE
                                               (render-bst BST4))))

桩函数：;(define (render-bst t) (square 0 "solid" "white"))

实现起来就和测试差不多了，需要注意node的key是number类型的，拼接字符串时需要将其转换为字符串：

如果树是false，那么为空树，则返回占位图MTTREE
否则就跟测试一样生成图像

(define (render-bst t)
  (cond [(false? t) MTTREE]
        [else
         (above (text (string-append (number->string (node-key t)) KEY-VAL-SEPARATOR (node-val t))
                                             TEXT-SIZE
                                             TEXT-COLOR)
                                       VSPACE
                                       (beside (render-bst (node-l t))
                                               HSPACE
                                               (render-bst (node-r t))))]))

运行后4个测试通过，可以在交互区输入(render-bst BST10)，查看渲染效果。

BST10 效果

Practice Problems

这一章的 Recommended Problems:

BST P2 - Sum Keys
- sum-keys-starter.rkt
- sum-keys-solution.rkt
BST P4 - Insert
- insert-starter.rkt
- insert-solution.rkt
BST P6 - Render BST With Lines
- render-bst-w-lines-starter.rkt
- render-bst-w-lines-solution.rkt

BST P2 - Sum Keys 题解

预计耗时：7 min / 简单

这道题让我们将一棵 BST 中所有的键加起来。这个函数的返回值是Natural，在判断时考虑空树：

如果为空，返回0
否则就将当前键加上左右子树递归的和（这样每次递归，都会将之后节点的键加起来）

;; BST -> Natural
;; sum all the keys in bst
(check-expect (sum-keys false) 0)
(check-expect (sum-keys BST3) (+ 3 1 4 7))

;<template from BST>

(define (sum-keys bst)
  (cond [(false? bst) 0]
        [else
         (+ (node-key bst)
            (sum-keys (node-l bst))
            (sum-keys (node-r bst)))]))

BST P4 - Insert 题解

预计耗时：30 min / 中等

这道题的难点在于我们应该想到在插入节点本身是在创建一个新的树，只不过刚好放个新节点进去，而不是在原有的树上进行修改。

在递归后，如果传入的树是空树，就意味着我们可以在这放新节点了，否则就在创建节点的同时顺便递归到左右子树：

(define (insert key val bst)
  (cond [(false? bst) (make-node key val false false)]
        [else
         (if (< key (node-key bst))
             (make-node (node-key bst) 
                        (node-val bst) 
                        (insert key val (node-l bst))
                        (node-r bst))
             (make-node (node-key bst) 
                        (node-val bst) 
                        (node-l bst)
                        (insert key val (node-r bst))))]))

BST P6 - Render BST With Lines 题解

预计耗时：45 min / 困难

绘图时总体上是垂直结构，包括当前节点、连接子树的线段和子树。

和之前某节一样，从上到下绘制即可，绘制到子树就直接递归，递归到空树就返回占位图MTTREE：

(define (render-bst bst)
  (cond [(false? bst) MTTREE]
        [else
         (above (text (string-append (number->string (node-key bst))
                       KEY-VAL-SEPARATOR
                       (node-val bst))
                      TEXT-SIZE
                      TEXT-COLOR)
                (lines (image-width (render-bst (node-l bst)))
                       (image-width (render-bst (node-r bst))))
                (beside (render-bst (node-l bst))
                        (render-bst (node-r bst))))]))