本模块将专注于自然数与函数，也会涉及到自我引用的部分。

学习目标

  • 能够设计对自然数进行操作的函数
  • 能够设计自然数的简单替代表示
以下内容涉及到的edX链接均不保证可访问性

Natural Numbers

自然数有无数个，所以我们可以借助自我引用来实现一个从给定自然数倒计时到0的函数。

在此之前，先介绍一个新表达式：add1和sub1。它们分别表示对自然数加1和减1，其使用方法和行为很像cons和rest。

比如(add1 0)的结果是1，而(sub1 1)的结果是0。你也可以嵌套着使用它们，比如(add1 (sub1 2))的结果是2。

下载来自edX的 naturals-starter.rkt 文件，里面给了一个倒数自然数的数据定义：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
;; Natural is one of:
;;  - 0
;;  - (add1 Natural)
;; interp. a natural number
(define N0 0)         ;0
(define N1 (add1 N0)) ;1
(define N2 (add1 N1)) ;2

(define (fn-for-natural n)
  (cond [(zero? n) (...)]
        [else
         (... ;n                           ;template rules wouldn't normally put this
          ;                            ;here, but we will see that we end up coming
          ;                            ;back to add it
          (fn-for-natural (sub1 n)))]))

;; Template rules used:
;;  - one-of: two cases
;;  - atomic distinct: 0
;;  - compound: (add1 Natural)
;;  - self-reference: (sub1 n) is Natural

下面还有两道题，让我们来看第一道，计算从0到n的自然数之和。

Design a function that consumes Natural number n and produces the sum of all the naturals in [0, n].

我们称该函数为sum，签名是Natural -> Natural，目的是produce sum of Natural[0, n]，然后测试有：

1
2
3
(check-expect (sum 0) 0)
(check-expect (sum 1) 1)
(check-expect (sum 3) (+ 3 2 1 0))  ; 倒序

桩函数：;(define (sum n) 0)。然后就可以从函数模板复制过来开始实现函数体了。

从函数的递归过程能发现，函数应该做到n + (n-1) + ... + 1 + 0，我们知道每次加的操作都是由一次递归调用来实现的，所以可以这样写n + (sum (sub1 n))：

1
2
3
4
(define (sum n)
  (cond [(zero? n) 0]
        [else
         (+ n (sum (sub1 n)))]))

接下来是第二道题，将传入的自然数转换为一个列表，列表的元素是从该自然数开始递减到0的所有自然数。

Design a function that consumes Natural number n and produces a list of all the naturals of the form (cons n (cons n-1 … empty)) not including 0.

我们称该函数为to-list，签名是Natural -> ListOfNatural，目的是produce (cons n (cons n-1 ... empty)), not including 0，然后测试有：

1
2
3
(check-expect (to-list 0) empty)
(check-expect (to-list 1) (cons 1 empty))
(check-expect (to-list 2) (cons 2 (cons 1 empty)))

写完桩函数;(define (to-list n) empty)，同理复制函数模板开始实现函数体。

确认终止条件，即zero? n满足时应当返回empty，否则就需要递归调用to-list，并将当前的n添加到列表：

1
2
3
4
(define (to-list n)
  (cond [(zero? n) empty]
        [else
         (cons n (to-list (sub1 n)))]))

从这两道题能看出不仅仅是列表能使用自我引用来遍历，自然数也可以做到这种效果。

ps: 该不会这语言的循环都是通过递归实现的吧？

A Parlor Trick

如果 Racket 语言没有自然数类型该怎么办？我们可以通过 HtDD 和 HtDF 来定义。下载来自edX的 new-numerals-starter.rkt 文件，描述说这个 Racket 语言甚至没有数字，但你需要自然数来编程。

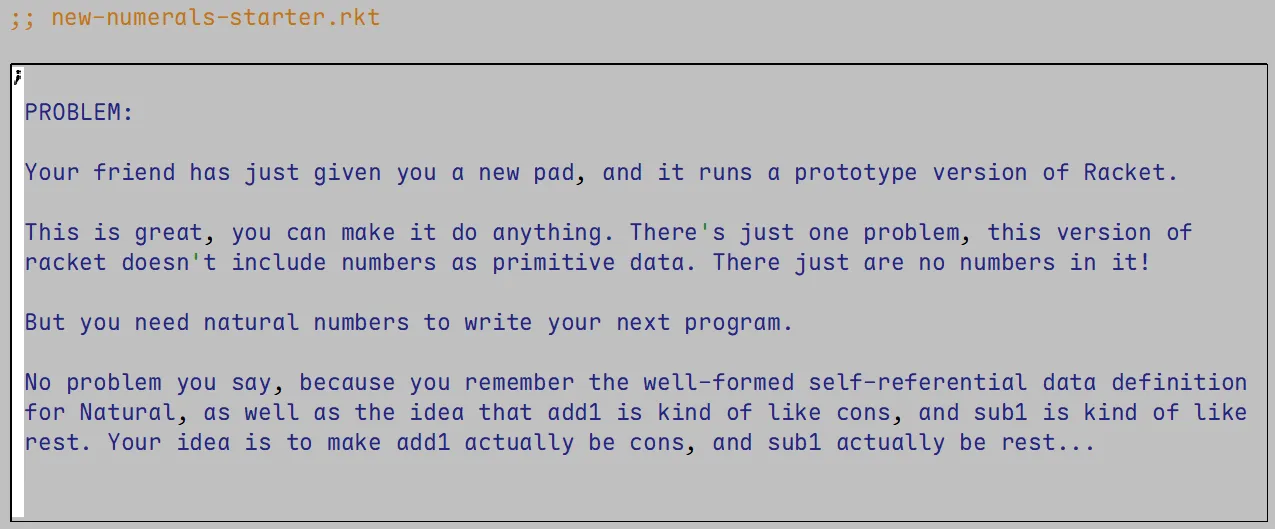
new-numerals-starter.rkt
new-numerals-starter.rkt

好在这个 Racket 还是有列表、字符串什么的，我们可以自己定义一个自然数试试，为了避免混淆，我们把它叫做NATURAL。这个NATURAL将会是一个列表，列表的元素都是"1"或者empty，通过列表长度来表示自然数的大小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
;; NATURAL is one of:
;;   - empty
;;   - (cons "1" NATURAL)
;; interp. a natural number, the number of "1" in the list is the number
(define N0 empty)         ;0
(define N1 (cons "1" N0)) ;1
(define N2 (cons "1" N1)) ;2
(define N3 (cons "1" N2)) ;3
(define N4 (cons "1" N3)) ;4
(define N5 (cons "1" N4)) ;5
(define N6 (cons "1" N5)) ;6
(define N7 (cons "1" N6)) ;7
(define N8 (cons "1" N7)) ;8
(define N9 (cons "1" N8)) ;9

在之前使用Natural时用到的zero?也可以实现了，只需要判断NATURAL是否是empty即可：

1
2
;; These are the primitives that operate NATURAL:
(define (ZERO? n) (empty? n))       ; Any -> Boolean

同理，add1和sub1也可以实现。比如ADD1给列表加一个"1"，SUB1则是借助rest表达式去掉列表的一个"1"：

1
2
(define (ADD1 n) (cons "1" n))      ; NATURAL     -> NATURAL
(define (SUB1 n) (rest n))          ; NATURAL[>0] -> NATURAL

ps: 之后的章节没要求就不需要写 Template rules used 了

函数模板可以写成逐渐减一的形式：

1
2
3
4
5
(define (fn-for-NATURAL n)
  (cond [(ZERO? n) (...)]
        [else
         (... ;n
          (fn-for-NATURAL (SUB1 n)))]))

自定义的NATURAL类型也需要基本运算的支持，比如加法ADD，它的签名是NATURAL NATURAL -> NATURAL，目的是produce a + b，测试有：

1
2
3
(check-expect (ADD N2 N0) N2)
(check-expect (ADD N0 N3) N3)
(check-expect (ADD N3 N4) N7)

桩函数：;(define (ADD a b) N0)。然后复制函数模板开始实现函数体：

1
2
3
4
(define (ADD a b)
  (cond [(ZERO? a) b]
        [else
         (ADD (SUB1 a) (ADD1 b))]))

看起来行为很奇怪，实际上这个函数的递归过程是将a逐渐减1，同时将b逐渐加1，直到a变成0时返回b。

减法同理：

1
2
3
4
5
6
7
8
9
10
11
;; NATURAL NATURAL -> NATURAL
;; produce a - b
(check-expect (SUBTRACT N2 N0) N2)
(check-expect (SUBTRACT N6 N2) N4)

;(define (SUBTRACT a b) N0)  ; stub

(define (SUBTRACT a b)
  (cond [(ZERO? b) a]
        [else
         (SUBTRACT (SUB1 a) (SUB1 b))]))

至此，我们已经实现了一个简单的自然数类型，并且支持了加减法运算。

Practice Problems

这一章的 Recommended Problems:

Naturals P2 - Decreasing Image 题解

预计耗时：15 min / 中等

这道题的递归思路比较绕，我们需要考虑到显示多个text是需要用beside来布局的，因此在递归的过程中需要将每个text都放在一个beside中，同时将下一个递归调用也放在里面。

ps: 以后可能只贴核心代码了

1
2
3
4
5
6
(define (decreasing-image n)
  (cond [(zero? n) (text "0" 20 "black")]
        [else
         (beside (text (number->string n) 20 "black")
                 (text " " 20 "black")  ; spacing
                 (decreasing-image (sub1 n)))]))

Naturals P3 - Odd from n 题解

预计耗时：15 min / 中等

这道题较简单，和之前用cons一样，我们只需要判断n是否为0，如果是0则返回empty，否则判断n是否为奇数，如果是奇数则将其添加到列表中，否则直接递归调用即可。

1
2
3
4
5
6
(define (odd-from-n n)
  (cond [(zero? n) empty]
        [else
         (if (odd? n)
             (cons n (odd-from-n (sub1 n)))
             (odd-from-n (sub1 n)))]))
参考资料
许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。