UBC - CPSC 110 - Self-Reference

我们在之前的学习中控制了猫和牛，但都是单个的。不仅如此，之前我们的数据定义整体上都是单个的。那么我们该如何控制多个数据呢，一些城市、一群牛？

这些信息被称为任意规模信息，也就是事先无法确定其大小的信息，也是现实中最容易遇到的情况。

ps: 好在本章的代码会比 HtDW 和复合类型简单

学习目标

• 能够运用列表机制来构建和解析列表结构
• 能够识别需要采用列表及结构体列表来表示的、规模不定的问题领域信息
• 能能够使用 HtDD、HtDF 和数据驱动模板配方处理此类数据
• 能够解释何为结构良好的自引用数据定义，并判断特定自引用数据定义是否符合良好结构要求
• 能够设计出处理并生成列表及结构体列表的函数
• 能够预测并识别数据定义中的自引用与操作该数据的函数中自然递归之间的对应关系

Introduction to Arbitrary Sized Data

我们之前学的所有内容，里面的数据结构都是定长 (Fixed Size) 的，但很多时候信息本身都是不确定的，数据又如何能确定呢？

List Mechanisms

本节会介绍列表 (List) 这个数据结构。顾名思义，它会存储一串某个类型的值。

我们可以在 DrRacket 里面写empty，它的意思也很顾名思义，就是空的列表（可以是任何类型）。但更准确地说，它通常被用于占位，因为cons表达式必须接受两个值，第二个值如果不存在就只能写个empty。

那么对于真正有数据的列表，我们可以使用cons表达式来构建，比如以下定义，之后可以运行下看看是什么输出：

1
2

(cons "Flames" empty)                 ; a list of 1 element
(cons "Leafs" (cons "Flames" empty))  ; a list of 2 elements

第一个cons构建了由一个元素组成的列表，这个元素的类型是String，后面的empty是空列表，它不计入元素数量。

第二个cons是由一个String和一个列表组成的列表，后面的列表里头虽说有empty，但整体上仍是由一个元素组成的列表，故它是两个元素的列表。

再试试这一句(cons (string-append "C" "anucks") empty)会得到什么：(cons "Canucks" '())。

这是因为在构建列表的时候，它会尝试将里面所有的表达式都变成确切的值。也就是说string-append会被执行，变成值然后替换表达式。同理，也可以试试(cons (square 10 "solid" "blue") (cons (triangle 20 "solid" "green") empty))。

如果接触过其他编程语言的列表，可能会觉得(cons 10 (cons 9 (cons 10 empty)))是两个元素，但实际上在 Racket 这里是三个，它不是算最外层元素数量的。

把代码简化为：

1
2
3
4

(require 2htdp/image)
(define L1 (cons "Flames" empty))
(define L2 (cons 10 (cons 9 (cons 10 empty))))
(define L3 (cons (square 10 "solid" "blue") (cons (triangle 20 "solid" "green") empty)))

为了防止混淆，这并不是在嵌套，上面的三个cons实际上会得到：

• "Flames"和'()
• 10、9、10和'()
• (square 10 "solid" "blue")的图像、(triangle 20 "solid" "green")的图像和'()

需要注意的是，cons本身其实就是一种复合类型的构造器，支持传入两个字段来组成列表。这就是有些同学可能会觉得为什么要嵌套声明列表。

列表的构建说完了，接下来就是它的相关操作。我们在学习数据结构时总是如此。

先是(first L1)，这一行会得到列表L1的第一个元素，即"Flames"。相对的(rest L1)会返回L1第一个元素之后的所有元素。可以试试将L1换成L2或L3来体验。

那么我们该如何获取第二个、第三个这种确切位置的元素呢？不同于其他编程语言下标的概念，这里只能通过first和rest表达式凑出来。比如：

1
2

(first (rest L2))         ; get the second element of L2
(first (rest (rest L2)))  ; get the third element of L2

ps: 有点怪只能说这个设计

最后就是empty?表达式，这个表达式后面接受一个参数，判断列表是不是empty，比如(empty? empty)的返回结果就是true，而(empty? L1)之类就是false。

List Data Definition

本节将会讲述列表的数据结构设计，在下一节探讨它的函数设计。在此之前，下载来自edX的 cat-starter.rkt 文件。

quidditch-starter.rkt

我们将要设计一个记录你最喜欢的魁地奇 (Quidditch，《哈利·波特》系列中重要的空中团队对抗运动) 队伍，需要先为它设计一个数据定义。

将光标移动到注释框的下方，然后在 DrRacket 上方工具栏找到Insert，点击展开后选择Insert Comment Box，就能得到一个注释框。然后按照这个操作再加一个。我们先列举下信息：

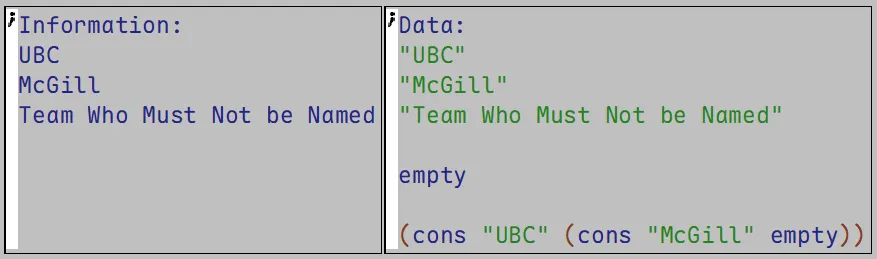
首先，有三个队：UBC、McGill和Team Who Must Not be Named (教授注：第三个不是指 UofT)。将这些信息放在第一个框。

然后就是由信息得到的数据结构，大概是(cons "UBC" (cons "McGill" empty))，第三个就是无名。

最后汇总如下：

Information & Data

之后再提一行，在程序的下方真正开始设计数据结构。我们将这个类型称为ListOfString，和枚举相似，它也是one of的，但有个比较有意思的点：

1
2
3
4

;; ListOfString is one of:
;;   - empty
;;   - (cons String ListOfString)
;; interp. a list of strings

有没有发现这个数据定义的第二个情况出现了它自己，这被称为自我引用 (Self-reference)。尝试自行梳理下为什么会这么写，可以看看它的例子是什么：

1
2
3

(define LOS1 empty)
(define LOS2 (cons "McGill" empty))
(define LOS3 (cons "UBC" (cons "McGill" empty)))

每个例子都符合该数据定义，LOS1直接符合第一种情况，而LOS2就先符合第二种情况，然后内部又符合第一种，LOS3同理。

以LOS2为例，它是怎么符合的：

• 首先是(cons "McGill" empty)，根据定义，它很像第二种情况，但我们不确定。
• 观察内部结构，存在一个String和一个empty，我们知道ListOfString确实有empty的情况。
• 那么它的结构实际上可以是(cons String ListOfString)，故满足。

会发现这个ListOfString有可能会呈现无限嵌套的情况，每个ListOfString类型都有可能为空，或者是由ListOfString组成的。这种感觉也可以被称之为递归 (Recursion)，之后的函数设计也会触及这一概念。

接下来就是函数模板设计，这里不需要那么绕，因为one of下面只有两种情况，那就在cond表达式写两个Q A就行：

1
2
3

(define (fn-for-los los)
  (cond [Q A]
        [Q A]))

唯一需要注意的是模板规则，empty其实是atomic distinct，而第二种情况就是cons表达式返回的值的类型，即compound：

1
2
3
4

;; Template rules used:
;;   - one of: 2 cases
;;   - atomic distinct: empty
;;   - compound: (cons String ListOfString)

借此，我们就知道如何完善刚刚的模板。第一个Q实际上是在判断传来的los是不是empty，而第二个Q其实就是else的情况：

1
2
3
4
5

(define (fn-for-los los)
  (cond [(empty? los) (...)]
        [else (... (first los)   ; String
                   (rest los))]  ; ListOfString
        ))

数据定义部分代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

;; ListOfString is one of:
;;   - empty
;;   - (cons String ListOfString)
;; interp. a list of strings
(define LOS1 empty)
(define LOS2 (cons "McGill" empty))
(define LOS3 (cons "UBC" (cons "McGill" empty)))

(define (fn-for-los los)
  (cond [(empty? los) (...)]
        [else (... (first los)   ; String
                   (rest los))]  ; ListOfString
        ))

;; Template rules used:
;;   - one of: 2 cases
;;   - atomic distinct: empty
;;   - compound: (cons String ListOfString)

Function Operating on List

本节会从上一节最后写的数据定义开始，为这个列表设计函数。问题如下：

Problem

如果传入的ListOfString含"UBC"，那么就返回true，那么称这个函数为contains-ubc?吧。

由题可知，它的函数签名是ListOfString -> Boolean，目的是produce true if los includes "UBC"。然后就是它的测试，我们可以参考ListOfString这个数据结构的例子来写：

1
2
3
4
5
6

;; ListOfString -> Boolean
;; produce true if los includes "UBC"
(check-expect (contains-ubc? empty) false)
(check-expect (contains-ubc? (cons "McGill" empty)) false)
(check-expect (contains-ubc? (cons "UBC" empty)) true)
(check-expect (contains-ubc? (cons "UBC" (cons "McGill" empty))) true)

它的桩函数是(define (contains-ubc? los) false) ; stub，也可以此测试下程序现在能不能跑。

从ListOfString的函数模板复制过来，函数名改为contains-ubc?，开始编写函数体：

• 对于empty的情况，我们应该直接返回false，因为空列表不可能含有"UBC"
• 对于有其他元素的情况，我们需要仔细思考下该怎么写：
  • 如果(first los)就是"UBC"，意味着这个列表确实存在"UBC"，那么就返回true。
  • 但是如果第一个元素不是，该怎么考察剩下的元素有没有"UBC"呢？

这将是本节最绕的地方，可能对于*剩下的元素有没有"UBC"*这个问题暂时摸不着头脑。但是我们可以看看当前函数的签名，你会发现就是ListOfString -> Boolean。

这是否意味着，有没有一种可能，我们可以在contains-ubc?函数调用contains-ubc?？

因为这个函数的目的就是判断一个ListOfString是否存在"UBC"，那我们可以让函数自己调用自己，让我们这么写else的A：

1
2
3

[else (if (string=? (first los) "UBC")
          true
          (contains-ubc? (rest los)))]

如果没转过弯，可能会觉得这难道不会一直在判断一个列表是否存在"UBC"呢？不会死在那吗？实则不然。

仔细观察这个部分，if表达式会判断当前列表的首项是不是"UBC"，如果不是，再将剩下元素传给下一个contains-ubc?。也就是说第二个contains-ubc?并没有拿到完整列表，它少了第一项。以此往复，下一个contains-ubc?永远都会比上一个少一项，这样就能判断剩下的元素究竟是空还是首项为"UBC"。

这被称为递归，简单理解就是一个函数会自己调用自己。

递归有去有回，它该怎么回来呢？假如(contains-ubc? (rest los))这个表达式被执行了10次，也就是说这个函数自身调用自己了9次，那么：

• 当列表本身被穷尽还没找到"UBC"，那函数必然会到达(empty? los)分支，返回false
• 当列表的首项是"UBC"，它会返回true

这个函数不会无限调用下去，它总是会到达一个终点，终点的布尔值会让这一切回到最初的函数中，返回出来。

Revising the Recipes for Lists

我们接触到了list的定义和操作，本节将会复盘前两节我们学到的内容。在此之前，下载来自edX的 quidditch-recap-starter.rkt 文件。

自我引用在定义中引用自身，像一个数据结构在绕圈子，同时递归则是函数调用自身，像一个函数在绕圈子。

打开代码文件后，我们能从your favorite Quidditch teams发现这个信息包含着随机 (Arbitrary) 数量的队伍，这也代表着它需要一个不定长度的列表来存储。

往下看看到ListOfString的定义，和之前的ListOfString一样，它也是一个自我引用的数据定义。我们可以看到它的两个情况：

• empty，属于base case，表示空列表
• (cons String ListOfString)，属于self-reference case，表示一个String和一个ListOfString的组合

对于测试来说，这两个case都需要覆盖到。

它在被处理的时候很可能会绕圈，但为什么最终会停下呢？就是因为base case的存在。每次调用contains-ubc?，它都会减少一个元素，直到它到达空列表。

它的函数模板其实并不完整，让我们重新看下：

1
2
3
4

;; Template rules used:
;;   - one of: 2 cases
;;   - atomic distinct: empty
;;   - compound: (cons String ListOfString)

我们实际上是要递归地处理一个列表的，这个模板并没有体现出这一点。我们需要在最后注明它的self-reference，也就是：

1
2
3
4
5

;; Template rules used:
;;   - one of: 2 cases
;;   - atomic distinct: empty
;;   - compound: (cons String ListOfString)
;;   - self-reference: (rest los) is ListOfString

再让我们看到函数设计部分。列表的测试也需要覆盖到两个case，同时self-reference case需要依赖base case来终止。

1
2
3
4

(check-expect (contains-ubc? empty) false)
(check-expect (contains-ubc? (cons "McGill" empty)) false)
(check-expect (contains-ubc? (cons "UBC" empty)) true)
(check-expect (contains-ubc? (cons "McGill" (cons "UBC" empty))) true)

对于递归函数，可能会有同学不太能梳理过程，以下是过程详解：

Detailed Explain

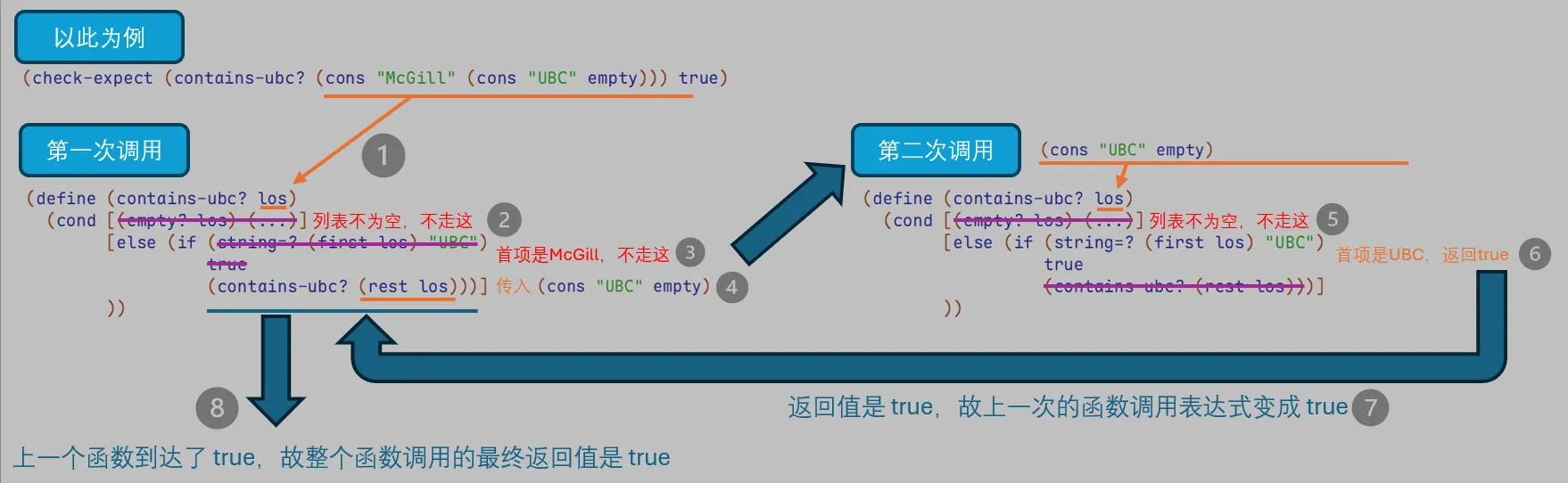
Designing with Lists & Positions in List Templates

我们将从来自edX的 designing-with-lists-1-starter.rkt 文件开始：

designing-with-lists-1-starter.rkt

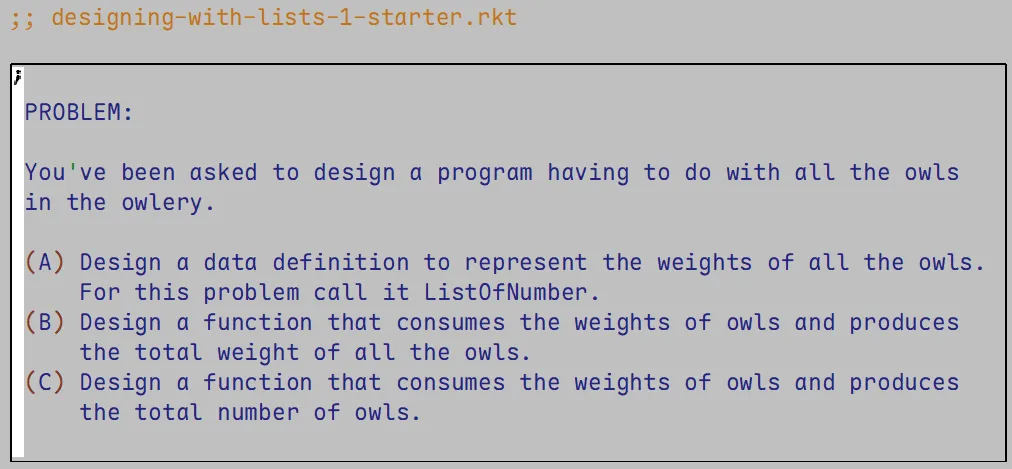
我们需要设计一个有关猫头鹰的程序，它需要：

• 一个数据定义用来保存所有猫头鹰的重量，称为ListOfNumber
• 一个函数，接受ListOfNumber，返回所有猫头鹰的总重量
• 一个函数，接受ListOfNumber，返回所有猫头鹰的数量

猫头鹰的数量自然是不确定的，所以它的数据结构需要是一个列表。我们可以先写下数据定义：

1
2
3
4

;; ListOfNumber is one of:
;; - empty
;; - (cons Number ListOfNumber)
;; interp. each number in the list is an owl weight in ounces

它的例子需要包含base和self-reference两种情况：

1
2

(define LON1 empty)
(define LON2 (cons 60 (cons 42 empty)))

之后就是函数模板。这次我们需要在模板中形成递归的关系：

1
2
3
4
5

(define (fn-for-lon lon)
  (cond [(empty? lon) (...)]
        [else
         (... (first lon)
              (fn-for-lon (rest lon)))]))

以及它的模板规则，记住需要加入self-reference：

1
2
3
4
5

;; Template rules used:
;;  - one of: 2 cases
;;  - atomic distinct: empty
;;  - compound: (cons Number ListOfNumber)
;;  - self-reference: (rest lon) is ListOfNumber

接下来就是函数设计部分。让我们再回顾下第二个需求：

一个函数，接受ListOfNumber，返回所有猫头鹰的总重量

我们可以称这个函数为sum，它的签名是ListOfNumber -> Number，目的是produce sum of weights of owls in lon。它的测试需要覆盖到所有情况：

1
2
3
4
5

;; ListOfNumber -> Number
;; produce sum of weights of owls in lon
(check-expect (sum empty) 0)
(check-expect (sum (cons 60 empty)) 60)
(check-expect (sum (cons 60 (cons 42 empty))) (+ 60 (+ 42 0)))  ; 格式对应

它的桩函数是;(define (sum lon) 0) ;stub，也可以此测试下程序现在能不能跑。

成功后再将函数模板复制过来，函数名改为sum，开始编写函数体：

• 对于empty的情况，我们应该直接返回0，因为空列表的总和是0
• 对于有其他元素的情况：
  • 如果(first lon)就是当前猫头鹰的重量，那么我们可以将它加到总和上。
  • 但是如果有多个猫头鹰，我们需要将剩下的猫头鹰的重量也加上。

1
2
3
4
5

(define (sum lon)
  (cond [(empty? lon) 0]
        [else
         (... (first lon)          
              (sum (rest lon)))]))

我们需要为empty情况返回0，而对于else情况，我们需要将首项的重量加上剩下猫头鹰的总重量，而剩下的重量该如何计算呢？请放心交给下一次递归调用的sum：

1
2
3
4

(define (sum lon)
  (cond [(empty? lon) 0]
        [else (+ (first lon)           ; 首项的重量
                 (sum (rest lon)))]))  ; 剩下猫头鹰的总重量

第三个需求是：

一个函数，接受ListOfNumber，返回所有猫头鹰的数量

可以称这个函数为count，它的签名是ListOfNumber -> Natural，目的是produce total number of weights in consumed list。它的测试需要覆盖到：

1
2
3

(check-expect (count empty) 0)
(check-expect (count (cons 12 empty)) (+ 1 0))                  ; 1个猫头鹰
(check-expect (count (cons 35 (cons 12 empty))) (+ 1 (+ 1 0)))  ; 2个猫头鹰

桩函数是;(define (count lon) 0) ; stub，测试下程序能不能跑。

再将函数模板复制过来，函数名改为count，编写函数体：

• 类似于我们刚刚的sum函数，对于empty的情况，我们应该直接返回0，因为空列表的数量是0
• 对于有其他元素的情况：
  • 如果(first lon)是一个猫头鹰的重量，那么我们可以将它计入数量。
  • 但是如果有多个猫头鹰，我们需要将剩下的猫头鹰的数量也加上。

数量的累加和总和不同，它是一个+ 1，因为每次递归调用都会有一个猫头鹰的重量被计入数量：

1
2
3
4
5

(define (count lon)
  (cond [(empty? lon) 0]
        [else 
         (+ 1 
            (count (rest lon)))]))

在思考列表相关的函数设计时，请相信递归能解决问题，自己调用自己不是什么黑箱。

Practice Problems

这一章的 Recommended Problems:

• Self-Reference P2 - Double All
  • double-all-starter.rkt
  • double-all-solution.rkt
• Self-Reference P3 - Boolean List
  • boolean-list-starter.rkt
  • boolean-list-solution.rkt
• Self-Reference P5 - Largest
  • largest-starter.rkt
  • largest-solution.rkt
• Self-Reference P6 - Image List
  • image-list-starter.rkt
  • image-list-solution.rkt

1
2
3
4
5
6
7
8
9
10
11
12
13
14

;; ListOfNumber -> ListOfNumber
;; double every number in the given list
(check-expect (double-all empty) empty)
(check-expect (double-all LON2) (cons  120 (cons 84 empty)))
(check-expect (double-all (cons 10 (cons 20 (cons 50 empty))))
              (cons 20 (cons 40 (cons 100 empty))))

;(define (double-all lon) empty) ;stub
;<template from ListOfNumber>
(define (double-all lon)
  (cond [(empty? lon) empty]
        [else
         (cons (* 2 (first lon))
               (double-all (rest lon)))]))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

;; ListOfBoolean is one of:
;;  - empty
;;  - (cons Boolean ListOfBoolean)
;; interp. a list of boolean values
(define LOB1 empty)
(define LOB2 (cons true (cons false empty)))
#;
(define (fn-for-lob lob)
  (cond [(empty? lob) (...)]
        [else
         (... (first lob)
              (fn-for-lob (rest lob)))]))

;; Template rules used:
;;  - one of: 2 cases
;;  - atomic distinct: empty
;;  - compound: (cons Boolean ListOfBoolean)
;;  - self-reference: (rest lob) is ListOfBoolean

;; ListOfBoolean -> Boolean
;; produces true if all values in the given list are true or if the list is empty
(check-expect (all-true? empty) true)
(check-expect (all-true? LOB2) false)
(check-expect (all-true? (cons true (cons true (cons true (cons true empty)))))
              true)

;(define (all-true? lob) true)  ;stub
;<template from ListOfBoolean>
(define (all-true? lob)
  (cond [(empty? lob) true]
        [else
         (and (first lob)
              (all-true? (rest lob)))]))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

;; ListOfNumber -> Number
;; produce the largest number in the given list, or 0 if empty
;; ASSUMES that every element of lon is > 0
(check-expect (largest empty) 0)
(check-expect (largest LON2) 60)
(check-expect (largest (cons 10 (cons 20 (cons 50 empty)))) 50)

;(define (largest lon) 0) ;stub
;<template from ListOfNumber>

(define (largest lon)
  (cond [(empty? lon) 0]
        [else
         (if (> (first lon) (largest (rest lon)))
             (first lon)
             (largest (rest lon)))]))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

;; ListOfImage is one of: 
;;  - empty
;;  - (cons Image ListOfImage)
;; interp. a list of images
(define LI0 empty) 
(define LI1 (cons (circle 20 "solid" "red") empty))
(define LI2 (cons (circle 40 "solid" "blue") (cons (circle 20 "solid" "red") empty)))

#;
(define (fn-for-loi loi) 
  (cond [(empty? loi) (...)]
        [else
         (... (first loi)
              (fn-for-loi (rest loi)))]))

;; Template rules used: 
;; - one of: 2 cases
;; - atomic distinct: empty
;; - compound: (cons Image ListOfImage)
;; - atomic non-distinct: (first loi) is Image
;; - self-reference: (rest loi) is ListOfImage

;; ListOfImage -> Number 
;; produce total area of all images
(check-expect (total-area empty) 0)
(check-expect (total-area (cons (rectangle 2 4 "solid" "red")
                                (cons (square 3 "solid" "blue")
                                      empty)))
              17)

;(define (total-area loi) 0)  ;stub
;<template from ListOfImage>

(define (total-area loi) 
  (cond [(empty? loi) 0]
        [else
         (+ (* (image-width (first loi))
               (image-height (first loi)))
            (total-area (rest loi)))]))